26살에 재종반 수학 대표강사, 3년 간 30년 치 기출문제 폐관 수련 후기 2탄
게시글 주소: https://o.orbi.kr/00066190271
1탄은
안녕하세요. 반갑습니다. 오르비 아이디에 등록한 전화번호를 개인적으로 사용할 수 없게되어 탈퇴했는데... 탈퇴하고나니 댓글이 많더라고요. 암살 당한것은 아닙니다. ㅎㅎ
2탄 시작합니다.
=====================================================================
[해설지가 뭐 이래...? 해설이 아니라 계산지 아닌가....? (feat. 수능 13번)]

2024학년도 수능 13번
도형 문제의 풀이는 연역적으로 풀지 않으면 항상 헤매게 되는 문제입니다. 그 이유는 기하에는 왕도가 없기 때문이죠?ㅎㅎ 운이 좋으면 풀리고 운이 안좋으면 안풀리고, 잘 보이는 날은 풀리고 잘 안보이는 날은 안풀리고...
그런데 수능 문제를 이런식으로 출제하지는 않겠죠? 운이 좋으면 풀 수 있있고 그렇지 않으면 풀 수 없는? 평가원에서 정해놓은 성취기준은 그런 것일리가 없습니다.
EBS의 해설을 보겠습니다.

갑자기 선분AC의 길이를 구합니다. 왤까요? 이 해설지는 사실 '해설'이 아닙니다. 문제를 해설하고 있는 것이 아니라 답을 향해 가는 풀이 또는 계산집이죠. 사실 선분AC의 길이를 구해야하는 이유를 설명하고 구하기 시작해야하는데 그냥 대뜸 구해버립니다. 그리고나서

S1을 구하고

Sin(각ACD)도 구하고, R도 구하고...
즉, 선분AC의 길이, Sin(각ADC), R을 모두 구해서 답을 냅니다. 이것은 아마도 답을 내는 과정이나 계획을 모두 다 마친 상태에서 연산하는 단계만 서술한 것이라고 보이는데... 그래도 조금 많이 이상합니다. 만약 둘다 구해야한다면 꼭 저런 모양(분자에 R 분모에 사인값)으로 구하라고 해야 했을까요?
다시 풀어 보겠습니다.
문제만 먼저 보면 원이 있고 그 안에 내접하는 삼각형이 있고 그 삼각형과 변 AC를 공유하는 각A가 60도인 삼각형이 있습니다.
맞나요? 고개가 끄덕여지시나요?
고개가 끄덕여 지면 논리가 꼬이기 시작합니다. 그 이유는 그림만 보고 나름대로 도형을 정의 했기 때문입니다.
이렇게 나름대로 정의 하면 작도하는 순서가 달라져서논리가 깨질 수 있습니다. 아마.. 헤매기 시작하겠죠?
문제 풀이의
첫번째는
문제 읽기 단계입니다.
도형 문제에서는 무엇보다 문제가 중요합니다. 그 이유는 도형이 어떤 순서로 정의 되었는가에 따라 구할 수 있는 것들이 결정되기 때문입니다.
이 문제는 처음에 사각형이 있습니다. 그 안에 대각선이 생겨 두 삼각형이 생깁니다. 그리고 그 중 하나의 삼각형의 외접원이 그려진 것입니다. 이해가 되시나요?
(아마 도형문제를 그림 먼저 보고 풀다가 안풀려서 문제 읽었더니 풀리던, 이런 경험있죠?)
두번째는
문제 설계 단계입니다.
1) 무엇을 물어 보았는가?

2) 단서를 이용한 조건의 해석
- 조건을 만족하는 식을 구합니다.
- 우선 S_2는 주어진 단서와 구하는 것을 보고 넓이를 나타내려고 한다면 선분AD*선분CD*Sin(각ADC)로 구하겠죠?
- 그리고 S_1을 구해야하는데 각과 길이 두개가 주어져 있으니 선분AC를 구해서 넓이를 구하면 되겠습니다. 이제 드디어 길이 AC를 구해야하지요.
(그전에 길이 AC를 구하는 것은 이상하죠? 만약에 주어진 정보만 가지고 아무 방향을 잡지 않고 구한다면, 길이 AC만 구하는 것은 이상합니다. 각과 길이 두개를 가지고 다른 각을 구할 수도 있는데 나머지 길이만 구한다고요?)
- 그럼 이제 조건을 표현해보면

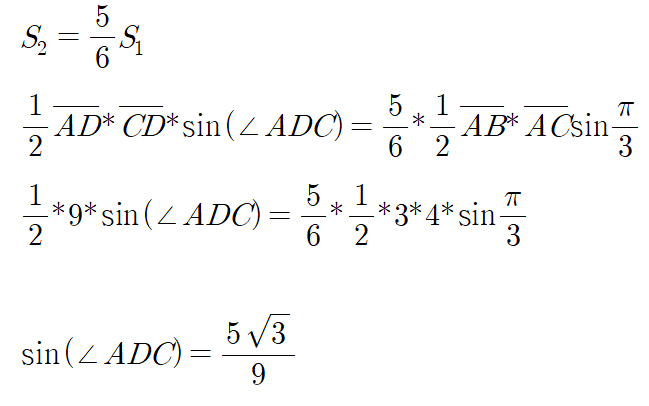
- 일때,
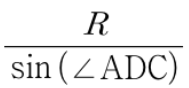

를 구해야 합니다.
3) 이제 답을 내는 연산을 합니다. 조건을 해석했으니 이를 이용하여, 구해야하는 것을 재구성 해볼까요?
- R은 위에 구했던 선분AC와 각ADC로 찾을 수 있겠네요.
-

이므로 구해야하는 것은
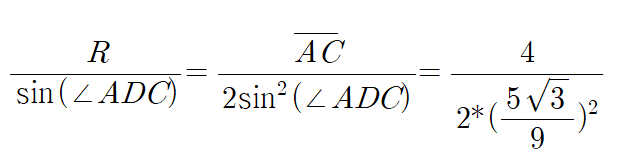

이렇게 답을 내겠죠?
세번째는
답을 확인하는 단계입니다.
방법은 여러가지가 있습니다. 풀이를 역연산 해본다거나, 나온 답의 각과 길이를 이용하여 주어진 정보나 조건과 같은가 확인해 볼 수도 있겠습니다. 또한 다른 풀이를 찾아볼 수도 있습니다. 이 과정에서는 EBS의 풀이처럼 반지름을 구해서 역으로 확인할 수도 있을것입니다.
답지를 보기전에 이미 내가 맞았는가 틀렸는가를 알 수 있어야 시험장에서 만점을 받을 수 있습니다.
풀이를 다 하고 보면 단 한 번의 연산도 허투루 하지 않았습니다.
우리가 다양한 풀이를 추구하는 것도 좋은 공부겠지만 문제 출제의 의도에 맞게 풀이를 해야 과한 연산을 줄일 수 있을 것입니다.
논리적으로 풀고, 해야하는 기본적인 연산을 연습하는 것이
계산량을 줄이려고 새로운 공식을 늘이는 것보다 훨씬 더 유리하지 않을까요?
문제 풀기 전에 설계를 하고 풀이를 시작해봅시다.
문제풀이의 시간은 아마도...
| 생각하는 시간 | 계산하는 시간 |
| 1 | 9 |
| 2 | 7 |
| 3 | 3 |
문제를 어떻게 푸시겠습니까?
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
다들 멋있게 찍은건데 왜 현우진 혼자 ㅡㅅㅡ 이러고있는 표정이냐 ㅋㅋㅋㅋㅋ...
-
저는 완전 개백수라서 현타가 좀 오네요 아침에 일어나서 웹소설 보고 애니 보니까...
-
9명모집이고 아직 14명 안들어옴 7등 8등 차이 0.01점 ㄷㄷ
-
신촌엔 대체 얼마나 커플이 많을까.. 에브리데이 히트데이일꺼야
-
원래 처음 재수 초반때 그 전해 화룡점정 풀면서 머리 깨졌었는데 0
갑자기 킬러가 없어졌어요
-
ㅈㄱㄴ 생12는 완전 다르잖음 내신으로는 했는데 둘다 수능으로는 어떤지 궁금...
-
대학교 1학년입학을 (1학년)2학기부터다닐수있나요? 1
서경대 모델연기학과합격하고바로군대가서 현재복무중입니다 (합격하고 바로군휴학해서...
-
1.쾌변을 눌 수 있게 된다 2.탐구시간때 화장실에서 큰일을 보고 와도 시간이...
-
솔직히 수학 너무 아까운데 진짜 올핸 감 유지만 해놓고 가봐야지
-
커피 마신게 잘못됐나
-
(현 재수생) 1월부터 재수결정해서 기출 마더텅 풀고있습니다 경기도 살아서...
-
비문학 인강을 한번도 들어본적이 없어서 그읽그풀과 구조독해가 있다는거 정도만 알고...
-
작년에 수특, 내신으로 하긴 했는데 기억삭제로 노베행 너무 늘어져서 배수진 친단...
-
맞팔할사람 12
맞팔해주때염 ㅠㅠ
-
성대 지원한거 9
입학처에서 이름 수험번호 생년월일 쓰고 확인해봣는데 뭐 정보를 찾을수 앖다? 이러면...
-
250107 기출2109나 속도 조절 shift + 부등호 다음 문항 ctr +...
-
옳게된 세상 12
정시 80% 수시 20% 수시 학교 오픈, 교과 일반전형만 유지 가나다군 폐지...
-
무난한거라고 보시나요? 아니면 소수과치고는 에바?
-
고민이넹
-
서강대 경영 6
점공 들어올수록 빡세지네..
-
갑자기 컷 내려가서 불합 극초 떴는데 그걸 어케 신뢰함 ㄹㅇ 그냥 운명인거지 그치그치
-
이번에 윈터스쿨 독학 기숙 들어가는데 유용한 팁 있을까요?
-
프사 바꿨어융 9
-
둘다 붙으면 일반적으로 전자임? 둘다 추합으로는 붙을거 같아서
-
그거 숫자에 따라서 등수가 좀 많이차이나던데
-
내일이면 안정화되려나
-
오르새t랑 양승진t 수2기출 어떤분이 좋을까요??? 0
고민 많이 되네요 각각 톡징이 어떤가요???
-
넣었음 눈이 넘 건조해서
-
전설의 2004 수능 미노타우르스가 있네 무슨 말을 할지 벌써 기대됨..
-
심찬우t처럼 읽을때 왜?에 집중하시는 스타일인가요?
-
경제X 사문X 세계사X 동사정법세지한지생윤윤사중에서 무슨과목 2개가 좋을까요..?...
-
셈퍼 점공 2
왜 시대점공계산기에 있는 셈퍼점공이랑 오르비에 있는 2025 셈퍼점공이랑 다르게나오죠?
-
전 맨날가서 1시간 하고 오는데 근육 빨리 붙이고 싶으면 얼마나 해야하나요?
-
고경제 651? 0
ㅅㅂ 몰카임?
-
죽음에 관하여 오탁번 1 왼쪽 머리가 씀벅씀벅 쏙독새 울음을 울고 두통은 파도보다...
-
한겨례가 칼럼써서 죽임
-
점공 관련 질문 1
점공 넣는거는 실제 그 학과에 지원한 사람들만 넣을 수 있는건가요?
-
제가 이상한건가요? 선생님이 자꾸 돌아다니면서 애들 하나하나 하는지 안하는지 계속...
-
조용한거임?? 소수과는 문자돌려도 왜 깜깜무소식이죠 자꾸 기대하게 만드네
-
ㅇㅇ
-
2월달에 OT나 새터는 참석하나요? 학교 가봐야 아무도 없고, 그럼 친구도...
-
제가 학군지에 살아서 이렇게 느끼는 걸지 몰라도 집 근처 둘러보면 널린 게 학원...
-
ㅇㅇㅇㅇㅇ ㅅㅂ 정신나갈거같아
-
추천뱓야용!!
-
걍 고경제 쓸걸 3
쓴사람 존나부럽다...
-
마감 직전에 봤을때 2등/36명 이어씁니다 소수과인데다 아직 공개율도 적어서...
-
50%는 넘어야하지않겠나..
-
헬스완뇨 0
힘들군
-
이런거 보통 남자들도 좋아하지않나



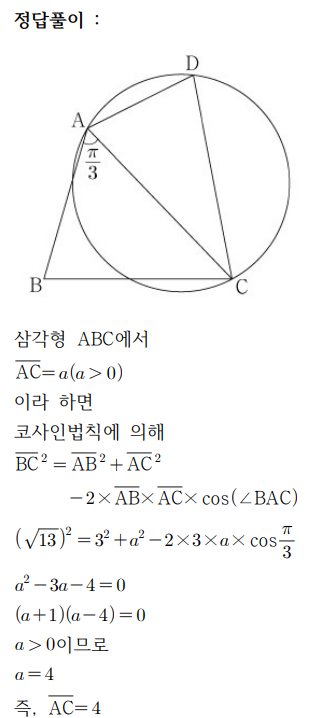



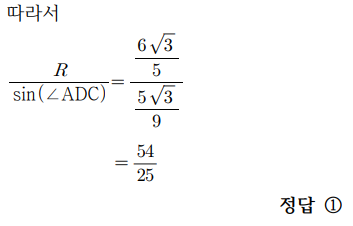
















































부활하셨군요
네 ㅎㅎ 관심 감사합니다!풀이의 이유를 명확히 제시해주는 선생님이 정말 좋은 선생님이라고 생각해요
그런 점에서 쌤 응원합니다
감사합니다. 행복하세요!
잘 읽었습니다. 요즘 수능에서 준킬러라 불리는 것들은 깊은 개념보다는 빠른 상황해석을 요구하는 경우가 많더라고요. 한번 사고 회로가 꼬이면 10분 이상씩 잡아먹는 게 고민이었는데(어떻게든 풀어내도 딱히 수학 실력이 올랐다는 느낌은 안들더라고요) 방향성을 설정하는 데 도움이 되었습니다 감사합니다. ㅎㅎ
막무가내로 조건들을 수집해서 어떻게든 끼워맞추던 게 제 풀이방식이었거든요 ㅋㅋ 수학 고수들이 문제 풀기 전 먼저 생각을 하라는 게 이런 의미였다니...
도움이 되었다니 기분이 좋네요! ㅎㅎㅎ 문제를 풀이를 시작하기전 풀이 계획을 잡는 것에 고민하는 시간을 길게 가져보면 좋을것 같습니다.
개인적인 질문 드려도 괜찮을까요?
질문이야... 얼마든지요! 답변을 해드릴 수 있는 내용이라면 답변드리겠습니다.
국어강의는 누구 들으셨나요?
으ㅎㅎㅎㅎ
OBAR 해석법이네요
저렇게 읽어야 수학의 본질이 뚤리는데..
OBAR 해석법이 뭐에요?? 자세히 찾아보고 싶어요